package mainI like it because I only ever declare a single integer variable, and the rest goes through chans. This solution is inspired by Haskell's concise "fib = 0:zipWith (+) fib (1:fib)". Any comments are most welcome. In particular, if there were a way to accomplish it (in the same style) without the buffered chans, that would be pretty cool (though I'd be a bit surprised, since it doesn't seem possible at first glance).
import "fmt"
func dup3(in <-chan int) (<-chan int,<-chan int,<-chan int) {
a,b,c := make(chan int,2),make(chan int,2),make(chan int,2);
go func() { for { x := <-in; a <- x; b <- x; c <- x } }();
return a,b,c
}
func fib() <-chan int {
x := make(chan int,2);
a,b,out := dup3(x);
go func() { x<-0; x<-1; <-a; for { x<- <-a + <-b } }();
return out
}
func main() {
x := fib();
for i:=0; i<10; i++ { fmt.Println(<-x) }
}
Tuesday, December 01, 2009
Fibonacci in Go
I've been playing around with Go a bit. Here's what I think is the most Go-like solution to producing the Fibonacci sequence.
Tuesday, November 17, 2009
Oscilloscope Pong

This was originally my final project for my undergraduate electronics lab. Now that I've finally defended my PhD, I've got some free time and am getting around to posting it. I'd been meaning to write up for a long time (about 7 years!). Of course, after writing it up in LaTeX, that still doesn't help with blogging, since TeX/EPS/PDF isn't such a great format for web viewing. Fortunately, before I hunkered down to write my thesis I somehow converted all these figures into PNG (I haven't the slightest idea how I did it anymore - anything I try lately looks terrible). You can download the PDF version here.
Introduction
The very first arcade game was Pong, created in the late 1970s. In its time, it was the height of digital technology. We return to this historic video game from a slightly different point of view. In the following pages we will construct an entirely analog version of Pong that can be played using a modern oscilloscope with an X-Y setting (which draws channel 1 on the X axis and channel 2 on the Y axis).Circuits
Here we look at the circuit from the top-down, starting with the big picture fitting all the subcircuits together, and then analyzing each individual subcircuit.Big picture
In Pong, there are three objects which must be drawn: the ball and the two paddles. We select the object to draw using a very fast triangle wave. At the extents, either paddle is drawn. In the middle, the ball is drawn. This is represented in the figure below. The lines CB, CP1, and CP2 serve as controls, allowing the corresponding signals (Bx,y, P1, and P2, respectively) to pass on to the scope only when the control is high. Thus, at any time, we need exactly one of CB, CP1, or CP2 to be high.
The main circuit consists of two parts. We need to have an output for the scope x position and the scope y position, respectively, shown in "Scope Output" below.

Analog Switch
The main workhorse of an analog Pong is the analog switch, denoted in the above schematics as a crossed circle, as shown in the figure. Using a series of analog switches, we can draw multiple objects on the oscilloscope at once. The analog switch we use here is constructed from an op-amp and an nJFET shown in the figure "Analog Switch" below. It allows the input signal to pass if and only if the control lead is above +5V. The input is sufficiently blocked when the control is grounded. More discussion of this circuit is given in the next section. We can add the output from several analog switches using an op-amp addition circuit.
Control Signal
The control signals CB, CP1, and CP2 are generated from a master control signal C. This master control signal, as explained above, is simply a fast triangle wave (I've forgotten the frequency), generated by the circuit shown in "Output Control" below. We then generate CP1 and CP2 by comparing C to 5V, such that CP1 is high when C<-5V and CP2 is high when C>+5V. We must be very careful to prevent any possible overlap in the control signals. Thus, we generate CB as CP1+CP2, as shown below.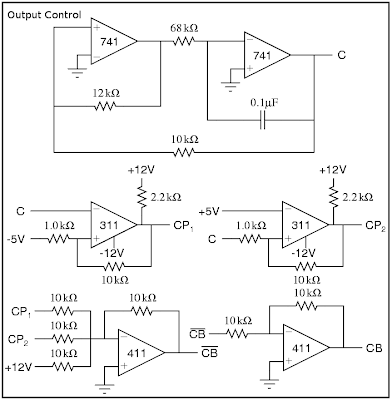
Ball Position
We generate the ball position from a pair of slow (1/3 to 3Hz) triangle waves, shown in "Ball Position" below. These circuits each have a pair of potentiometers: R1 and R3 adjust the y- and x-amplitudes of the ball's motion and should be adjusted so that the ball's motion fills the oscilloscope screen, currently designed to be ±4V vertically and ±5V horizontally. R2 and R4 adjust the y- and x-speeds.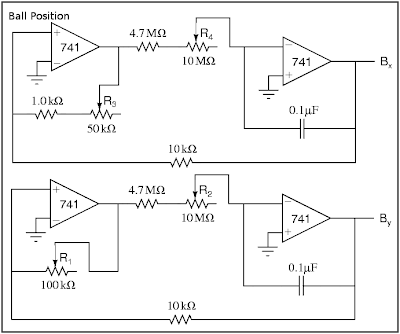
Paddles
The vertical paddle positions are given by the lines P1 and P2, which we construct with a voltage divider, shown below in "Paddles". The potentiometers R8 and R9 should be large and easy to adjust (i.e., a joystick) and are used to move the paddles up and down. R6 and R7 control the vertical range of the paddles' motion (i.e. from -3V to +3V). Whlie there's no theoretical problem with using them, small potentiometers are hard to find, so we insert an op-amp buffer to decrease the output impedance instead.In order to make the paddle appear as more than a point, we add a fast (about 10kHz, so that the entire length of the paddle is drawn each time CPi is high) triangle wave signal LEN, shown also in "Paddles", to the Y output whenever we're drawing the paddles (i.e. when CB-bar is high). The potentiometer P5 controls the size of the paddles (around ±1V).
The horizontal positions are fixed at ±5V, that is, either edge of the screen.

Power Supply
We assume that the breadboard setup includes ±12V and ground, but we may need to generate our own ±5V lines, which can be done cleanly with a simple voltage divider fed through a 411 op-amp buffer (shown in PDF only).Improvements
Hit detection and scoring
The circuit shown so far is more of an interactive movie than a game. The controls can alter the size and position of the paddles, but can't react differently if the ball is hit or missed. I attempted to add logic to deal with this case using a D-type flip flop as shown in "Hit Detection" below, where B'x and B'y are sent to the scope instead of Bx and By. As the design currently stands, it simply hides the ball until a reset button is pressed. The inputs Di must change when By is within a paddle length of the Pi, and the clock signals CLKi should go off only at the very tips of the master control signal C. Finally, the "g" and "r" diodes should be green and red LEDs to show who missed.
Unfortunately, this addition caused some impedance problems and smeared the whole picture terribly, and I was never able to fix it.
Dynamic ball speeds
One other modification that would be nice would be to allow the ball speeds (at least the vertical speed) to change based on how the paddles hit it. If there was some way to lock-in a "resistance" based on, say, By-Pi at a certain point, rather than using semi-fixed potentiometer, then it might not be so difficult. Likely we'd want another sort of flip flop, but I never looked very far into how that might be accomplished.Monday, June 29, 2009
ICFP Contest 2009
It's been just about a year and I haven't posted anything... I've got a few drafts of posts, so maybe I'll try to get one or two of them done this summer. Anyway, this weekend was the ICFP contest. I don't have near as much to say about it as last year, mainly since I only spent about 16 hours working on it, starting Sunday afternoon, along with David Roundy and some help from our friend Joanna.
It was an interesting problem this year. Teams were required to implement a virtual machine to run "OrbitVM" binaries provided by the contest organizers. Then the interesting part was writing a controller to perform certain tasks in orbital dynamics (in 2d), ranging from doing a simple Hohmann transfer to change the radius of a circular orbit, to flying around to collect a number of satellites. The physics seems like it would be interesting to work out, but we didn't really get around to it. Just thinking about it, though, an orbit about a single body in 2d has four parameters: the semimajor axis (for simplicity, I'll assume it's an ellipse), the eccentricity, the orientation of the major axis, and the phase along the orbit. These can be calculated from the position and velocity (x, y, vx, and vy) of a satellite. On the controls side, there are only two "knobs" we can control: the impulses in the tangential and radial directions. So we can see that it can't be trivial to transfer from any orbit to any other, and in fact we could probably define some sort of metric to describe how distant two particular orbits are (minimizing a cost function composed of total impulse and time required). Of course, even with just elliptical orbits, this is well beyond the realm of tractability, but if it were implementable, it would lead to some sort of traveling salesman problem, except that the distances varied with time in incommensrate ways. What a mess... (not to mention the real problem also had a moon to make the orbits less than elliptical, and was integrated with a large enough time step to make the integration error somewhat important)
That's enough abstraction. I enjoyed working on the contest, although we only solved the first sub-problem of performing a Hohmann transfer. With only one day, there really wasn't any chance to outdo last year's performance, but we decided to have some fun with it anyway. The original plan was to do it in postscript, so our team name was "Paper Jam in Tray 3". But it turned out that rolling our own IEEE doubles was just too tedious (postscript only supports singles natively), and the extra precision was important (at least, in the Verlet integrator David wrote). So instead we implemented all of our logic in the OrbitVM virtual machine. It wouldn't have been completely terrible to write straight assembler, but I felt it would be more fun to write a compiler, so we embedded an OrbitVM a compiler into Haskell. It was a pretty simple compiler, and would have benefited greatly from more developed control structures (the VM itself was rather lacking in control structures: every instruction was executed and every mutable value in memory was written to exactly once per time step; the only control structure was a conditional copy that could copy from one of two memory locations, depending on the result of a comparison). We did implement a static data type, Vector, that simplified dealing with 2d coordinates and velocities, but the part that was most frustrating to deal with was maintaining state from one time step to the next; with some more thought I believe it could have been improved quite a bit.
We also had to find some way to connect these programs together. A perl script provided good plumbing and also allowed us to intercept the communication and visualize the trajectories with ghostscript, as well as allowing us to inspect some of the internal quantities to see what was going wrong.
I spent a number of hours, after we finally got some points on the scoreboard, trying to get the second problem, but without a more sophisticated development system, it was difficult to try new ideas and we never quite managed to catch any moving satellites, although I was able to fly by them briefly (just the velocities were all wrong by the time the positions matched up). The basic strategy I used (at least for the case of both satellites in circular orbits) was to calculate the required "phase difference" for when to start the transfer such that I landed on the second orbit just as the target was passing by. This got me close, but not quite close enough, and I never figured out how to do the tiny tweaks of the orbit to close in. It might be fun to make a "real-time" orbit simulator to get some intuition for how to do this. There would be some orbiting circle and the goal would be to pilot a spacecraft into an orbit within the circle using a combination of radial and tangential burns. Though maybe once you're looking at it in the rotating frame it would just be a piece of cake. We never actually looked at the rotating frame, which was maybe our problem...
In case you're curious, our source tree is available at http://pages.physics.cornell.edu/~shicks/darcs/icfp09/.
The problem
It was an interesting problem this year. Teams were required to implement a virtual machine to run "OrbitVM" binaries provided by the contest organizers. Then the interesting part was writing a controller to perform certain tasks in orbital dynamics (in 2d), ranging from doing a simple Hohmann transfer to change the radius of a circular orbit, to flying around to collect a number of satellites. The physics seems like it would be interesting to work out, but we didn't really get around to it. Just thinking about it, though, an orbit about a single body in 2d has four parameters: the semimajor axis (for simplicity, I'll assume it's an ellipse), the eccentricity, the orientation of the major axis, and the phase along the orbit. These can be calculated from the position and velocity (x, y, vx, and vy) of a satellite. On the controls side, there are only two "knobs" we can control: the impulses in the tangential and radial directions. So we can see that it can't be trivial to transfer from any orbit to any other, and in fact we could probably define some sort of metric to describe how distant two particular orbits are (minimizing a cost function composed of total impulse and time required). Of course, even with just elliptical orbits, this is well beyond the realm of tractability, but if it were implementable, it would lead to some sort of traveling salesman problem, except that the distances varied with time in incommensrate ways. What a mess... (not to mention the real problem also had a moon to make the orbits less than elliptical, and was integrated with a large enough time step to make the integration error somewhat important)
Our solution
That's enough abstraction. I enjoyed working on the contest, although we only solved the first sub-problem of performing a Hohmann transfer. With only one day, there really wasn't any chance to outdo last year's performance, but we decided to have some fun with it anyway. The original plan was to do it in postscript, so our team name was "Paper Jam in Tray 3". But it turned out that rolling our own IEEE doubles was just too tedious (postscript only supports singles natively), and the extra precision was important (at least, in the Verlet integrator David wrote). So instead we implemented all of our logic in the OrbitVM virtual machine. It wouldn't have been completely terrible to write straight assembler, but I felt it would be more fun to write a compiler, so we embedded an OrbitVM a compiler into Haskell. It was a pretty simple compiler, and would have benefited greatly from more developed control structures (the VM itself was rather lacking in control structures: every instruction was executed and every mutable value in memory was written to exactly once per time step; the only control structure was a conditional copy that could copy from one of two memory locations, depending on the result of a comparison). We did implement a static data type, Vector, that simplified dealing with 2d coordinates and velocities, but the part that was most frustrating to deal with was maintaining state from one time step to the next; with some more thought I believe it could have been improved quite a bit.
We also had to find some way to connect these programs together. A perl script provided good plumbing and also allowed us to intercept the communication and visualize the trajectories with ghostscript, as well as allowing us to inspect some of the internal quantities to see what was going wrong.
I spent a number of hours, after we finally got some points on the scoreboard, trying to get the second problem, but without a more sophisticated development system, it was difficult to try new ideas and we never quite managed to catch any moving satellites, although I was able to fly by them briefly (just the velocities were all wrong by the time the positions matched up). The basic strategy I used (at least for the case of both satellites in circular orbits) was to calculate the required "phase difference" for when to start the transfer such that I landed on the second orbit just as the target was passing by. This got me close, but not quite close enough, and I never figured out how to do the tiny tweaks of the orbit to close in. It might be fun to make a "real-time" orbit simulator to get some intuition for how to do this. There would be some orbiting circle and the goal would be to pilot a spacecraft into an orbit within the circle using a combination of radial and tangential burns. Though maybe once you're looking at it in the rotating frame it would just be a piece of cake. We never actually looked at the rotating frame, which was maybe our problem...
Download
In case you're curious, our source tree is available at http://pages.physics.cornell.edu/~shicks/darcs/icfp09/.
Wednesday, July 16, 2008
ICFP Contest 2008
(Browse or download the code at http://www.physics.cornell.edu/~shicks/icfp08)
So, I just finished sleeping off a "double all-nighter" for the ICFP Programming Contest. The task this year was to write a controller for a Mars rover. The program would connect to a server which would send it periodic telemetry updates and then it would send back instructions, either Accelerate, Brake, Left, or Right. I had tried to get a team together for this contest, but it was apparently a busy weekend and all my programmer friends had other plans.
After thinking about the problem (and my situation as a solo entry) for a few minutes, I decided it would be interesting to see if I could write it in TeX. Lately I've been writing a whole lot of TeX for Andy Ruina, as well as for a macro package (inlinedef) I recently submitted to CTAN, so the idea didn't seem too crazy ("When all you've got is a hammer...").
Of course, to figure out how far off from the target we were, I needed an arctangent function, and this is definitely not provided by TeX. So I set about to write \atan (I would have called it \atan2, since that's really what it was, but names can't have numbers normally). Really about the only thing that was feasible to do here was a polynomial expansion. I opened up Octave and plotted tan(x) next to x+x^3/3 (naturally) from 0 to pi/4, and it didn't look that great. But it looked like I could probably do a better job by just tweaking the cubic coefficient by hand. In the end, I settled on atan(x)~x-.2x^2 (sure, I could have optimized it without much difficulty - in fact I just did and it turns out that -.17297x^2 works slightly better, though I would have done really better with the cubic term -.26219x^3, which I've now implemented, or even better, -.05x^2-.18796x^3 -- thanks SciPy). So I coded this up and it seemed to get the job done, anyway. I downloaded the sample server and maps and watched how it worked on the simplest map, with no craters to crash into and die. It didn't quite work, but a little tweaking of the numbers made a big difference and I was able to get home. I went to bed Saturday morning around 7am (EDT) and got 7 hours sleep before I had to wake up for sailing and then having some people over to my apartment, all of which kept me busy until about 10pm.
It took a long time to get this code to behave as I wanted. Often I'd find the rover turning the wrong direction entirely, driving straight into craters, driving straight for the outside edge of the map, or once, hitting the same boulder repeatedly until time ran out. If I knew how to do it, it would be neat to stitch together all these bloopers and make a 2-3 minute youtube video of the bloopers and then see them gradually improve to the final result (yay for darcs that that's even possible). Most helpful in this process was Octave (a free MATlab clone) - at one point I coded up a debugging message that printed out Octave code to plot a graph with lines from the current position to the target, the new trajectory, and the obstacle in question. Often the new trajectory was worse than the original one and I could go step-by-step to figure out why that was happening. Eventually when all these little errors were debugged, I had a code that did exactly what I wanted it to do, but it still did no better than if I'd done nothing at all to avoid the obstacles. This was the way it went for most of Sunday (I took an hour nap before church, but otherwise spent the whole time working). People on the IRC channel were talking about A*-algorithms and such, but that was much too smart for me - I had a hard enough time just getting to where I wanted to go when there weren't obstacles - so I just kept plugging away.
Around dinner time, Geoff called and suggested I go to his house to watch a movie. I was trying out a new idea I had, much simpler than many of the others: implement a two-state machine. The rover is either in the running state, where it's turning towards home, or else it's in the swerving state, where it's avoiding an object. If the rover sees an object in the way, closer than a certain distance (determined by the time it would take to turn 90 degrees at max speed, but this foolishly ignored the unknown turning acceleration, which turned out to be pretty important, and could probably have been discovered without too much difficulty... if only I had a team), then it would start swerving away from the object. The key point here was that we were looking ahead of us, rather than looking always toward home. So surprisingly we stopped running into things! I eventually converged on the logic that it would keep turning until it was no longer obstructed, and then it would go into a tunnel-vision mode, heading straight forward until the object it was swerving past was directly perpendicular with its direction, so that we know it's passed before trying to turn back home. This revealed all sorts more bugs as my dot product apparently just didn't work, but eventually I got it all worked out so that by the time I went over to Geoff and Erin's, I had a working version to show them, swerving back and forth and reaching the goal about 80% of the time. Around this time I also called up David Roundy and told him what I was up to. He suggested a few things, including the team name I finally settled on (actually, I think this was his sister-in-law), The Lone TeXnician, and a bit about what I should do with my README file.
You can browse or download the code if you like. I've cleaned it up a little bit since submission, in particular using better trig approximations I worked out while writing this. If you want to run it, you'll probably need a *nix system. You'll also need to download the simulation server and maps (remember to use '-v' to get a visualization window). Pass the '-l' option to `texsocket` to run in LaTeX and get the PDF output. Unfortunately I don't deal with disconnecting servers very well in the version I submitted, so it doesn't actually produce the PDF (more than) half the time and never gives any hint as to why.
Edit: pictures and pdf documents
Edit 2: Shortly after the contest ended, I learned of pdftex's built-in timers, which one of the commenters noted. I also learned about /dev/tcp (although the contest LiveCD didn't have it compiled into bash anyway). With all that working together, I could presumably have written a completely TeX solution (although blocking vs. non-blocking network access would certainly be an issue... maybe if TeX forked an extra process of itself...). Also, since it's now public knowledge, I did indeed win the judges prize.
I've turned off comments because of spam. If you want to say something, feel free to email me.
So, I just finished sleeping off a "double all-nighter" for the ICFP Programming Contest. The task this year was to write a controller for a Mars rover. The program would connect to a server which would send it periodic telemetry updates and then it would send back instructions, either Accelerate, Brake, Left, or Right. I had tried to get a team together for this contest, but it was apparently a busy weekend and all my programmer friends had other plans.
After thinking about the problem (and my situation as a solo entry) for a few minutes, I decided it would be interesting to see if I could write it in TeX. Lately I've been writing a whole lot of TeX for Andy Ruina, as well as for a macro package (inlinedef) I recently submitted to CTAN, so the idea didn't seem too crazy ("When all you've got is a hammer...").
Initial Work
The first problem that arose immediately after I decided on TeX was that TeX has no network access. So I had to make a small concession in writing a small Perl wrapper to do the networking. In the end, this file would be under a hundred lines, so I considered it a necessary, but minimal, evil. On one or two occasions I thought about farming some computation out to the Perl wrapper (such as trig), but in the end decided to stay pure. I learned about the IO::Socket::INET library and used the IPC::Open2 package to open a socket and a two-way pipe to a TeX process. Then we just read the TeX output and wait for special commands. Occasionally we'll write "WANT" which is a signal to Perl that TeX is ready for the next packet of information. Or else "HERE: " which tells Perl to send the following signal back to the server. I coded this up and found that it was really all that was needed to connect TeX to the world. Next, we needed to interpret the data. The server sent plain text data in the form ofI 600.0 600.0 30000 60.0 ... ;with a different number of mostly-numerical arguments depending on which letter came first (this determined what kind of datum it was). Since TeX can already parse this sort of thing, I figured the best bet would be to just make these letters all 'active characters' inside TeX so that they acted like control sequences. This worked well because occasionally multiple commands arrived on the same line, and so we'd need to do something special to account for this otherwise, but now it was automatic. More often, however, TeX's requests for data were more frequent than the packets were arriving (this is a good thing), but TeX's request (\read) is blocking, so we just sent an empty line in this case.
Math
If I were writing this in a real language like C++ or Haskell, one of the first things I would do would be to find or write a convenient data type for 2d vectors, since they're all over the place here. But TeX doesn't even really support things as simple as floating-point multiplication or (even worse) division. So I started by kyping some fixed-point multiplication and division macros I remembered seeing on comp.text.tex a while back (posted in the mid-90's by Donald Arseneau). I also kyped Kevin Hamlen's sqrt macro from his CDLabels package that I'd remembered him boasting about. These simple tools in hand, I was able to start making some real progress. I defined a bunch of counters (integer variables) and lengths (fixed-point numbers) and some booleans to keep track of what time it was, where we were and wanted to go, and which way we wanted to turn (wow, alliteration). Then, each time we received telemetry updates, I would turn towards the target if we were off by more than 20 degrees, brake if we were off by more than 90, and accelerate otherwise.Of course, to figure out how far off from the target we were, I needed an arctangent function, and this is definitely not provided by TeX. So I set about to write \atan (I would have called it \atan2, since that's really what it was, but names can't have numbers normally). Really about the only thing that was feasible to do here was a polynomial expansion. I opened up Octave and plotted tan(x) next to x+x^3/3 (naturally) from 0 to pi/4, and it didn't look that great. But it looked like I could probably do a better job by just tweaking the cubic coefficient by hand. In the end, I settled on atan(x)~x-.2x^2 (sure, I could have optimized it without much difficulty - in fact I just did and it turns out that -.17297x^2 works slightly better, though I would have done really better with the cubic term -.26219x^3, which I've now implemented, or even better, -.05x^2-.18796x^3 -- thanks SciPy). So I coded this up and it seemed to get the job done, anyway. I downloaded the sample server and maps and watched how it worked on the simplest map, with no craters to crash into and die. It didn't quite work, but a little tweaking of the numbers made a big difference and I was able to get home. I went to bed Saturday morning around 7am (EDT) and got 7 hours sleep before I had to wake up for sailing and then having some people over to my apartment, all of which kept me busy until about 10pm.
An inverse heisenbug
According to the jargon file, a heisenbug is one that disappears when you try to debug it. In this case, my code worked okay, but when I tried to see what it was doing by turning on visualization, it suddenly stopped working as well. It wasn't too difficult to figure out that the visualization was slowing down the server so that it didn't deliver all the telemetry data in a timely way. so I decided that I needed better timing. It turns out that even turning on tracing to the log file in TeX is enough to reduce the resolution beyond workability, and in my final code, in later runs when there's a long list of obstacles, that starts slowing it down too much too. TeX doesn't have any sort of timing functions (\time returns the time to the minute that the typesetting began but is in fact constant). So again comes Perl to the rescue. Presumably I could have measured something like distance travelled at a known speed and backed out an estimate for the amount of time spent between iterations, but this would of course changed depending on the situation, so again, I felt justified in resorting to Perl here. Now whenever TeX asked Perl for data, we included a timestamp in the response to keep our own clock. This gave a much better resolution and we could then estimate where we were and make decisions about 10x as often. By 2am Sunday, the rover could make it home consistently on the easy map with no dangers, but usually fell into craters on the more complicated ones, so this was the next thing to be addressed.Collision avoidance
By far the most difficult (and frustrating) part of the contest was collision avoidance. I tried a number of things to make it smarter, but they all failed miserably. They typically did worse than before I tried to do anything. Generally, I tried the logic that at any time we've got a target we're shooting for, and if at any time there was a known obstacle between the current position and the target, we'd move the target to a place that wasn't hindered (now that I'm writing this, I see the error here much more clearly). Then we issue commands to steer us toward that new target. If ever the path home was unblocked, we'd try to go there instead.It took a long time to get this code to behave as I wanted. Often I'd find the rover turning the wrong direction entirely, driving straight into craters, driving straight for the outside edge of the map, or once, hitting the same boulder repeatedly until time ran out. If I knew how to do it, it would be neat to stitch together all these bloopers and make a 2-3 minute youtube video of the bloopers and then see them gradually improve to the final result (yay for darcs that that's even possible). Most helpful in this process was Octave (a free MATlab clone) - at one point I coded up a debugging message that printed out Octave code to plot a graph with lines from the current position to the target, the new trajectory, and the obstacle in question. Often the new trajectory was worse than the original one and I could go step-by-step to figure out why that was happening. Eventually when all these little errors were debugged, I had a code that did exactly what I wanted it to do, but it still did no better than if I'd done nothing at all to avoid the obstacles. This was the way it went for most of Sunday (I took an hour nap before church, but otherwise spent the whole time working). People on the IRC channel were talking about A*-algorithms and such, but that was much too smart for me - I had a hard enough time just getting to where I wanted to go when there weren't obstacles - so I just kept plugging away.
Around dinner time, Geoff called and suggested I go to his house to watch a movie. I was trying out a new idea I had, much simpler than many of the others: implement a two-state machine. The rover is either in the running state, where it's turning towards home, or else it's in the swerving state, where it's avoiding an object. If the rover sees an object in the way, closer than a certain distance (determined by the time it would take to turn 90 degrees at max speed, but this foolishly ignored the unknown turning acceleration, which turned out to be pretty important, and could probably have been discovered without too much difficulty... if only I had a team), then it would start swerving away from the object. The key point here was that we were looking ahead of us, rather than looking always toward home. So surprisingly we stopped running into things! I eventually converged on the logic that it would keep turning until it was no longer obstructed, and then it would go into a tunnel-vision mode, heading straight forward until the object it was swerving past was directly perpendicular with its direction, so that we know it's passed before trying to turn back home. This revealed all sorts more bugs as my dot product apparently just didn't work, but eventually I got it all worked out so that by the time I went over to Geoff and Erin's, I had a working version to show them, swerving back and forth and reaching the goal about 80% of the time. Around this time I also called up David Roundy and told him what I was up to. He suggested a few things, including the team name I finally settled on (actually, I think this was his sister-in-law), The Lone TeXnician, and a bit about what I should do with my README file.
The icing on top
By early Monday morning, all I had left to do was clean it up, package it, and make sure it worked on the LiveCD environment that would be used in judging. The latter part was actually a bit difficult and I had been working on and off the whole time to figure out how to install TeX on the system with neither internet connection (apt-get would have been too easy...) or sending in a 50MB tarball with all of the basic TeXLive ditribution in it. I eventually figured out how to get a 2MB portion of the distribution to work by copying files from my /usr/bin/ and /usr/share/texmf/ and running `texhash` over and over again. I spent most of the rest of my time on an extra feature I really wanted. I would use LaTeX's picture environment to draw a map of the planet and trace the path that the rover followed. It took a while to get this working - I started out trying to make a single picture per trial and had grouping issues. I switched to using a separate (but overlapping) picture for each thing I wanted to draw, but they didn't line up properly. I tried saving all the drawing commands to a token list so that I could draw the whole thing at once at the end of the trial, but token list operations are O(n) in the length, so I started lagging way behind and couldn't keep up with the server (it was real-time, remember). Ultimately, I tracked down all but a small issue which caused misalignment only later in the process. This was eventually fixed when I found the errors, both in the swerving code (as I should have realized when they started so late and the trajectory up until them was straight, but then it curved - if I had painted the two modes in different colors like I originally wanted to, it would have been even more blatantly obvious!). Both errors came from putting decimal numbers where an integer was expected (stupid non-typed languages...) resulting in the fractional part being typeset instead of used mathematically, and pushing the reference point away from where it belonged.Conclusion
I ended up submitting code that I was very proud of. It ignored the ravenous martians entirely, and had a hard time in some tight situations (and some not-so-tight), but in general it made its way home about as well as (or better than) you might expect for 1200 lines of TeX. I ended up getting 8 hours of sleep over the course of three nights, and promptly crashed for 17 hours.You can browse or download the code if you like. I've cleaned it up a little bit since submission, in particular using better trig approximations I worked out while writing this. If you want to run it, you'll probably need a *nix system. You'll also need to download the simulation server and maps (remember to use '-v' to get a visualization window). Pass the '-l' option to `texsocket` to run in LaTeX and get the PDF output. Unfortunately I don't deal with disconnecting servers very well in the version I submitted, so it doesn't actually produce the PDF (more than) half the time and never gives any hint as to why.
Edit: pictures and pdf documents
Edit 2: Shortly after the contest ended, I learned of pdftex's built-in timers, which one of the commenters noted. I also learned about /dev/tcp (although the contest LiveCD didn't have it compiled into bash anyway). With all that working together, I could presumably have written a completely TeX solution (although blocking vs. non-blocking network access would certainly be an issue... maybe if TeX forked an extra process of itself...). Also, since it's now public knowledge, I did indeed win the judges prize.
I've turned off comments because of spam. If you want to say something, feel free to email me.
Friday, June 22, 2007
PostScript libraries
I've been writing some PostScript lately, such as matrix multiplication routines: things that really belong in a library. So I spent a good chunk of time today writing some software for preparing postscript files to be libraries. I wrote a Perl script `curdle` which takes a PostScript file as input and compresses it to a binary encoding with no comments and minimal spaces. At some point I'll add a script which will rename long internal variable names (as directed by comments). Once the file is compacted, it can be run through encode85 (which I found on some random FTP site) and put into a resource file a big block of gibberish, which is then either included automatically by the PostScript viewer, or else pasted at the top of the PostScript file which includes it. In any case, it should help significantly with PostScript library version control. Especially when I automate the resource part and include a "built on" date in the header.
If you're interested you can get the most up-to-date version of it with darcs (or just browse to this directory):
darcs get http://www.physics.cornell.edu/~shicks/darcs/pslib/
If you're interested you can get the most up-to-date version of it with darcs (or just browse to this directory):
darcs get http://www.physics.cornell.edu/~shicks/darcs/pslib/
Tuesday, May 29, 2007
Blogger pain
I get frustrated when Blogger wants to "Save as Draft" whenever I hit Ctrl+D. I usually expect this keystroke to ask as delete. So I hit it often, and get annoyed when it loads a new page. So I fixed it. Here's another Greasemonkey script.
Firefox + Google Scholar + Cornell Library
So, I was sick of having to go through the CU Library homepage for every journal article I wanted to download at home. And so I wrote a quick and dirty plugin to add a link to each Google Scholar result to access it through the CU Library proxy automatically, this saving gobs of time (maybe someday as much time as I spent writing it in the first place!).
One (small) issue with this is that it only works if you're logged into CUWebLogin, but checking for that each time is very slow. So I actually make two links - the "login" link goes through the official channels while the other link attempts to bypass them and go directly to the article, so it should be quicker if you're already logged in. It probably wouldn't be too tough to edit it to work for a different school with a little investigation.
To use the plugin, you need to have GreaseMonkey, which is a pretty standard Firefox plugin allowing you to use any of a multitude of "user scripts" which are basically scripts people write to post-process webpages.
I also wrote a standalone plugin to add a button to the (right-click) context menu to access a page through the library, in case it came from somewhere other than Google Scholar. This one is only the slow access method, although it could be configured to access it quicker with enough demand.
At some point, I may integrate all this into a standalone plugin. And I may look into adding a configuration tool so that other university libraries will be usable (although I'd need help from others for this to work). For now, if you're at a different school and would like to try using this, talk to me and I'll see if I can hack together a version for you.
One (small) issue with this is that it only works if you're logged into CUWebLogin, but checking for that each time is very slow. So I actually make two links - the "login" link goes through the official channels while the other link attempts to bypass them and go directly to the article, so it should be quicker if you're already logged in. It probably wouldn't be too tough to edit it to work for a different school with a little investigation.
To use the plugin, you need to have GreaseMonkey, which is a pretty standard Firefox plugin allowing you to use any of a multitude of "user scripts" which are basically scripts people write to post-process webpages.
I also wrote a standalone plugin to add a button to the (right-click) context menu to access a page through the library, in case it came from somewhere other than Google Scholar. This one is only the slow access method, although it could be configured to access it quicker with enough demand.
At some point, I may integrate all this into a standalone plugin. And I may look into adding a configuration tool so that other university libraries will be usable (although I'd need help from others for this to work). For now, if you're at a different school and would like to try using this, talk to me and I'll see if I can hack together a version for you.
Installation
- Install Greasemonkey if you haven't already.
- Install the userscript for Google Scholar links.
- Install the browser plugin for the context menu:
Subscribe to:
Posts (Atom)
